PDF-Datei

ISO/BIPM-Leitfaden: Meßunsicherheit (Fussnote 1)

Dr. Wolfgang Kessel, Braunschweig

Zusammenfassung:

Ausgehend vom Begriff des Meßprozesses und der naiven Sicht der Meßunsicherheit wird die moderne GUM-Sicht der Meßunsicherheit dargestellt und der Zusammenhang zwischen der Standardmeßunsicherheit und der aus industriell-ökonomischer Sicht bedeutungsvollen erweiterten Meßunsicherheit diskutiert.

Abstract:

Starting from the concept of a measuring process and the naive view of measurement uncertainty the paper presents the modern GUM view of the measurement uncertainty and discusses the interdependence of the standard uncertainty of measurement and the expanded uncertainty of measurement mostly used in industry and trade.

Inhalt:

1 Einleitung

 Eine wesentliche meßtechnische Erfahrung ist, daß beim Vergleich von Meßwerten neben dem eigentlichen Wert auch eine Angabe über seine Verläßlichkeit bzw. seine Qualität benötigt wird. Eine solche Angabe wird sich in jedem Falle auf technisch-wissenschaftliches Wissen stützen, d.h. auf objektive Fakten. Da es sich um ein Urteil handelt, bleibt eine solche Angabe trotzdem subjektiv. Man kann erreichen, daß ein Qualitätsurteil allgemein akzeptiert wird, wenn die Art und Weise transparent wird, wie das Urteil zustande kommt. Die transparente Unsicherheitsanalyse hat das zum Ziel.

2 Der Meßprozeß

 Im Jahre 1992 wurde der Begriff der Meßunsicherheit durch den ISO/BIPM "Guide to the expression of uncertainty in measurement", kurz GUM, neu geprägt [1]. Er ist in der Zwischenzeit international als die Basis für die Bestimmung der Meßunsicherheit akzeptiert (Fussnote 2). Er wurde auch in das Dokument EAL-R2 [2]

der "European cooperation for Accreditation" als verbindlich bei Kalibrierungen übernommen. Er stützt sich auf Eigenschaften des Meßprozesses. Die Definition der Begriffe findet sich im VIM [3] und in der DIN 1319 [4].

Der Meßprozeß soll den Wert einer physikalischen, meßbaren Größe 

in Bezug auf eine Einheit feststellen. Diese Tatsache wird allgemein durch die Relation

    (1)
 

  • Wert, der durch die Messung ermittelt wird,
  - Einheit, in Bezug auf die der Wert ermittelt wird,
 


ausgedrückt. Diese Gleichung zeigt, daß das Wesen des Meßprozesses die Zuordnung eines Wertes durch Vergleich ist: Der Wert der Größe auf der rechten Seite wird mit Hilfe des Meßprozesses auf die Meßgröße links übertragen. Dieser Sachverhalt wird z.B. bei der Ermittlung des Wägewertes einer Masse, wie ihn Bild 1 zeigt, deutlich.

 

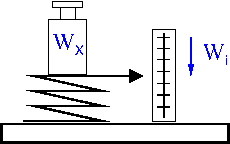
Bild 1: Ermittlung des Wägewertes einer Masse mit einer Waage
  - zu bestimmender Wägewert,
  - angezeigter Wägewert,
  - aufgrund einer Kalibrierung bekannte Abweichung des angezeigten Wertes vom anzuzeigenden (richtigen) Wert (Fehler der Anzeige). Ist die Waage nicht kalibriert, stellt diese Abweichung einen weiteren zu berücksichtigenden Anteil der unbekannten Abweichungen dar,
  - unbekannte Abweichung von der idealen Kennlinie,
  - unbekannte Abweichung aufgrund der endlichen Auflösung der Anzeige und des Nullabgleichs.
 
I.a. wird eine Messung, insbesondere wenn es sich um eine präzisere handelt, nicht aus einer so einfachen Zuordnung bestehen, wie sie Bild 1 darstellt. Es werden weitere Einflußgrößen eine Rolle spielen, wie z.B. die Temperatur der Umgebung, die Nicht-Linearität des Wandlers (im Bild die Feder), der die Meßgröße in die Anzeige transformiert, die Ungleichmäßigkeit der Anzeigeskala u.a.m. Das bedeutet jedoch nur, daß die unbekannten kleinen Abweichungen 

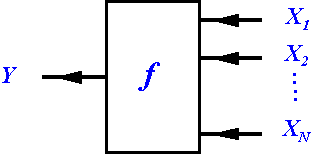
und  weiter in Summen entsprechender kleiner Abweichungen aufspalten. Die Grundstruktur des physikalischen Zusammenhanges von Bild 1 bleibt erhalten. Insgesamt ergibt sich bei einer Messung ein allgemeiner Zusammenhang wie ihn das Diagramm in Bild 2 zeigt:

 

Bild 2: Zusammenhang zwischen den Einflußgrößen und der Meßgröße
 
Es gibt eine Meßgröße ,

deren Wert zu bestimmen ist und zwar aus den Werten der Einflüsse . Der Zusammenhang wird durch die im Meßprozeß realisierte physikalische Relation - angedeutet durch den weißen Kasten - vermittelt. Mathematisch erfolgt die Zuordnung in einer Messung über die Modellfunktion der Auswertung:
 

    (2)
    - Meßgröße, deren Wert das Ziel der Messung ist, 
    - Einflußgrößen, die in die Ermittlung des Meßwertes  


eingehen, 
    - Anzahl der Einflußgrößen, 
    - Modellfunktion (mathematische Relation), mit der der Wert 
aus den Einflußgrößen ermittelt wird, 
 
Die linke Seite symbolisiert die Meßgröße, die rechte Seite den Konstruktionsmechanismus, nach dem aus den Einflußgrößen die Größe erzeugt wird, deren Wert zugeordnet wird.

3 Die naive Sicht : Unsicherheitsintervall
 


Es ist eine Grunderfahrung der Meßtechnik, daß eine Messung kein exaktes Ergebnis liefert. Das Ergebnis ist vielmehr mit einer Unsicherheit behaftet. Zur Angabe dieser Unsicherheit dient die Meßunsicherheit. Sie ist nach VIM (3.9) , GUM (2.2.3) und DIN 1319-T1 (3.6) zu definieren:

Die naive Sicht der Meßunsicherheit betrachtet den gesamten Bereich der verträglichen Werte als ein Unsicherheitsintervall, ohne die darin enthaltenen Werte zu wichten


 

    (3)
  , - obere und untere Grenze des Unsicherheitsintervalls.
 
Bild 3 verdeutlicht die Zusammenhänge.

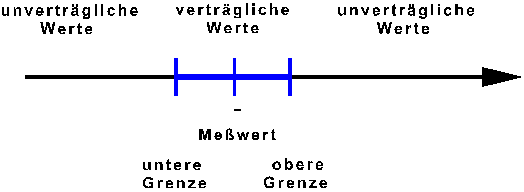
Bild 3: Kennwerte eines Unsicherheitsintervalles

 
Als Meßwert wird der arithmetische Mittelwert der beiden Grenzen angesehen
 

    (4)
 
und als Unsicherheitsmaß die Halbweite des Unsicherheitsintervalls
 

  . (5)
 
Diese Sicht der Meßunsicherheit ist für Messungen (z.B. Bild 1) recht brauchbar, bei denen nur wenige Einflußgrößen in der Zuordnung auftreten. Da die Unsicherheit in der Meßgröße durch die Unsicherheit in den Einflußgrößen entsteht, müssen die Grenzen für die Ergebnisgröße aus den Grenzen der Eingangsgrößen mit der Gleichung (2) berechnet werden.

Die Formeln für die dabei benötigten arithmetischen Operationen Addition, Subtraktion, Multiplikation und Division sehen zunächst recht einfach aus:
 

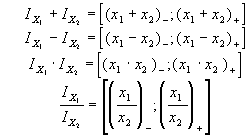    (6)
 


Geht man in die Details der Berechnung, so erhält man Gleichungen, die unübersichtliche Vertauschungen der Werte enthalten und eine Reihe von im Endeffekt doch recht unübersichtlichen Fallanalysen erfordern:
 

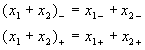    (6a)
 

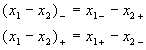    (6b)
 

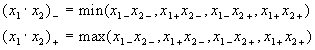    (6c)
 

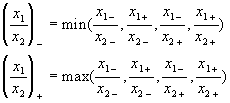    (6d)
 
Die naive Sicht der Meßunsicherheit ist daher nur für gewisse, recht grobe Klasseneinteilungen sinnvoll. Sie ist keine Basis für ein vielseitiges Qualitätsmaß. Der Rechenaufwand wird schon bei wenigen Einflußgrößen erheblich und ist für komplexere mathematische Ausdrücke z.B. für trigonometrische Funktionen ohne weitere Entscheidungsregeln bezüglich der Grenzen kaum noch durchführbar.

Ein Punkt entfaltet jedoch schon in der naiven Sicht seine volle Problematik: der Nachweis der Übereinstimmung eines Wertes mit einer Spezifikation. Wird die Meßunsicherheit mit einem Unsicherheitsintervall einbezogen, entsteht neben den Bereichen der Übereinstimmung und der Nicht-Übereinstimmung ein sog. Unsicherheitsbereich (oder besser Indifferenzbereich), wie ihn Bild 4 zeigt. Eine eindeutige Übereinstimmung bzw. Nicht-Übereinstimmung ist nur gegeben, wenn der Meßwert in den entsprechenden Bereichen liegt. Werte im Unsicherheitsbereich müssen entweder spezieller beurteilt [5] oder präziser bestimmt werden. Die Vorgehensweise wurde im Rahmenprogramm der MICROTECH 1996 eingehend diskutiert [6]. Die Regeln sind oder werden in der ISO EN DIN 14253 [7]

genauer festgelegt.
 

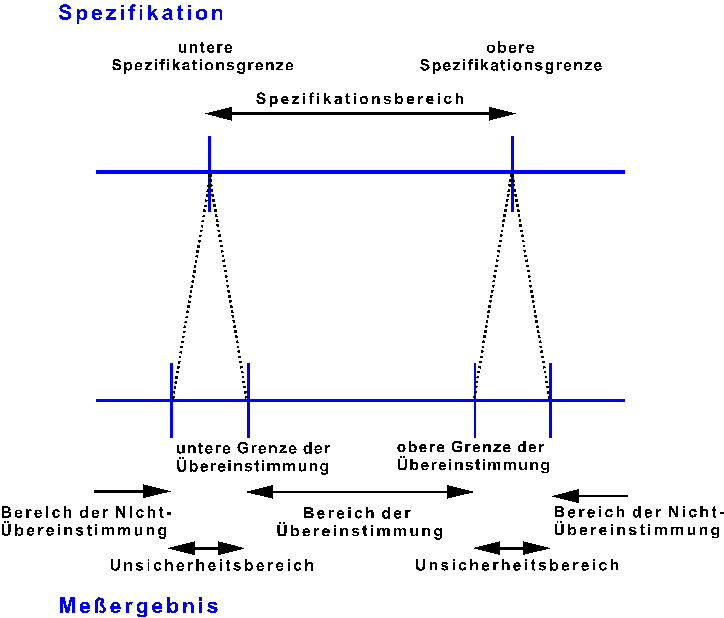
Bild 4: Bereiche der Übereinstimmung und der Nicht-Übereinstimmung eines Meßwertes mit einer Spezifikation, und Bereiche der Unsicherheit
 
Ein Problem zeigt sich bei der Behandlung präziserer Messungen mit vielen Einflußfaktoren. Die Gleichungen (6) liefern für die Meßgröße ein Unsicherheitsintervall, dessen Halbweite in den meisten Fällen gleich der Summe der Halbweiten der Unsicherheitsintervalle der einzelnen Einflußgrößen ist. Die Halbweiten werden so unrealistisch groß. Eine Erhöhung der Präzision, die ja stets mit einer Erhöhung der Anzahl der berücksichtigten Einflußgrößen einhergeht, bringt keine wesentliche Schrumpfung des Unsicherheitsintervalles der Meßgröße. Der Unsicherheitsbereich wird durch genauere Messungen kaum wesentlich schmäler. In der naiven Sicht der Meßunsicherheit bringt eine detailliertere Betrachtung der Messung und ihrer Einflußgrößen im wesentlichen keinen Gewinn. Ein Erweiterung des Übereinstimmungsbereiches eines gemessenen Wertes mit einer Spezifikation kann jedoch nur auf zwei Weisen erfolgen: in einer Neubewertung der Spezifikationen mit einer entsprechenden Erweiterung des Spezifikationsbereiches oder einer Verringerung der Meßunsicherheit. Eine Verringerung der Meßunsicherheit erreicht man nur durch eine Verbesserung der Meßmöglichkeit, was meist teuer oder aufwendig ist, oder durch eine realistischere Beurteilung der unbekannten Meßabweichungen, wie sie das GUM bietet.

 

 
4 Die GUM-Sicht : Standardmeßunsicherheit
 
Im GUM wird eine andere Sicht der Meßunsicherheit eingeführt. Die Angabe eines Unsicherheitsintervalles ist zu global. Sie berücksichtigt nicht, daß nicht alle mit den Meßbedingungen verträglichen Werte die gleiche Chance der Realisierung haben. Meist weiß man aus speziellen Kenntnissen bzw. grundsätzlichen Überlegungen, daß Werte nahe der Mitte des Unsicherheitsintervalles wahrscheinlicher sind als Werte nahe den Grenzen. Es gibt auch Fälle, in denen das umgekehrt ist. Das GUM geht von Verteilungen, genauer Wahrscheinlichkeitsverteilungen, der verträglichen Werte [8]

aus. Der Meßwert ist der mit der Verteilung gebildete Erwartungswert, die ihm beigeordnete Meßunsicherheit ist die Standardabweichung. Sie ergibt sich als die positive Quadratwurzel aus der Varianz:
 

(7)
(8)
- Meßwert, der der Größe  zugeordnet ist,
- Standardmeßunsicherheit, die dem Meßwert  beigeordnet ist,
 
symbolisiert eine der Größen der Modellbeziehung in Gleichung (2), inkl. der Ergebnisgröße . Die so bestimmte Meßunsicherheit wird Standardmeßunsicherheit

(engl. standard uncertainty of measurement) genannt. Zum einen, weil sie die Standardabweichung der Verteilung ist. Zum anderen beschreibt sie die mittlere Weite so grundsätzlich, daß sie in vielen Formeln auftritt.
 
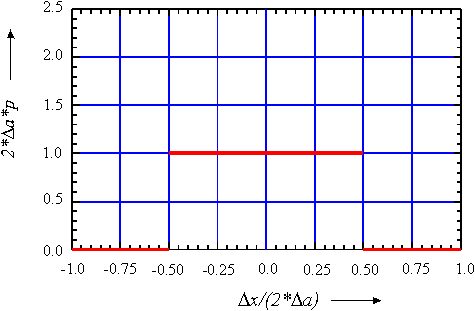
Die naive Sicht tritt auch in der GUM-Sicht teilweise wieder auf. Wenn man von den Werten einer Größe nur weiß, daß sie zwischen einer unteren  und einer oberen  Grenze liegen, sind alle Werte zwischen diesen Grenzen gleichberechtigt. Die magere Kenntnis führt zu der in Bild 5 dargestellten rechteckförmigen Verteilung.


 

Bild 5: Rechteckförmige Verteilung - Gleichverteilung der Werte zwischen einer unteren und einer oberen Grenze
 
Der Meßwert ist der gleiche wie in Gleichung (4); die ihm beigeordnete Standardmeßunsicherheit ergibt sich aus der Halbweite des Variabilitätsintervalles zu:


 

(9)
 
Eine rechteckförmige Verteilung wird man als Verteilung der Werte bei digitalen Anzeigen annehmen. Die halbe digitale Auflösung (halber Quantisierungsschritt) um den angezeigten Wert definiert die untere bzw. obere Grenze, bei der die Anzeige zum jeweils benachbarten Wert springt.


 
Der Übergang zu Verteilungen der Werte hat eine wichtige Folge. Die Verteilung der Werte einer Summe bzw. Differenz zweier Eingangsgrößen ist stärker um den Ergebniswert konzentriert. Bild 6 zeigt eine dreieckförmige Verteilung, entstanden aus der Differenz zweier rechteckförmiger Verteilungen gleicher Halbweite. Die Modellfunktion lautet
 

(10)
 
mit dem Ergebniswert
 

(11)
 
und der beigeordneten Standardmeßunsicherheit

.
(12)
 
 

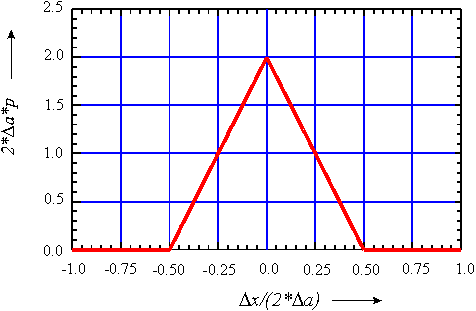
Bild 6: Dreieckverteilung - entstanden durch Faltung zweier rechteckförmiger Verteilungen gleicher Halbweite
 
Die Standardmeßunsicherheit hat für die Summe und die Differenz den gleichen Wert. Die Halbweite in Gleichung (12) ist die Halbweite der dreieckförmigen Verteilung. Sie ist das Doppelte der Halbweiten der gefalteten rechteckförmigen Verteilungen. Die Kurve zeigt, daß kleine Abweichungen vom Meßwert wahrscheinlicher sind als große. Der Meßwert kann aus verschiedenen Kombinationen der Eingangswerte gewonnen werden, die Grenzwerte jedoch nur aus einer, nämlich der Kombination der Grenzwerte selbst.


 
Für eine allgemeine Summe aus drei Eingangsgrößen mit rechteckförmigen Verteilungen gleicher Halbweite ergibt sich schon nahezu eine Gaußsche Glockenkurve. Das zeigt Bild 7 deutlich.
 

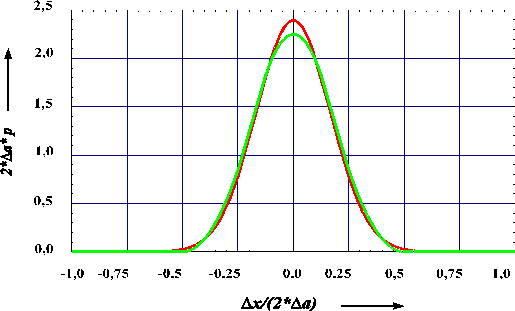
Bild 7:  Dreifach gefaltete Rechteckverteilung im Vergleich zur Normalverteilung gleicher Varianz.
 
Die Abweichungen von der Normalverteilung sind überall kleiner als 5%. Hier zeigt sich die Wirkung des zentralen Grenzwertsatzes. Er besagt, daß die Werte einer Summengröße eine Normalverteilung besitzen, wenn die Anzahl der Summanden hinreichend groß ist und ihre Varianzen, d.h. die Quadrate der Standardmeßunsicherheiten, sich nicht zu stark unterscheiden. Bei rechteckförmigen Verteilungen gleicher Halbweite reichen schon drei Größen aus.
 


 
5 Das Verfahren des GUM
 
Da die Meßunsicherheit immer einem Meßwert beigeordnet ist, ist die Meßunsicherheitsanalyse untrennbar mit der Bestimmung des Meßwertes verknüpft. Nach dem GUM erhält man den Meßwert durch Einsetzen der Werte der Eingangsgrößen in die Modellfunktion
 

(13)
- Meßwert, Ergebnis der Messung, 
- Eingangswerte, Werte der Einflußgrößen.
 
Das Quadrat der beigeordneten Standardmeßunsicherheit ergibt sich als Summe aus den Quadraten der Unsicherheitsbeiträge

der einzelnen Eingangsgrößen
 

(14)
- Unsicherheitsbeiträge der einzelnen Einflußgrößen.
 


Die Unsicherheitsbeiträge berechnen sich aus den Standardmeßunsicherheiten, die den Eingangswerten beigeordnet sind, durch Multiplikation mit den Sensitivitätskoeffizienten (engl. sensitivity coefficient)
 

(15)
- Sensitivitätskoeffizient bezüglich der Einflußgröße ,
- Standardmeßunsicherheit, die dem Eingangswerte  beigeordnet ist.
 
Über die Sensitivitätskoeffizienten kommt das Modell ins Spiel. Sie sind gegeben durch die partiellen Ableitungen der Modellfunktion nach den jeweiligen Eingangsgrößen.
 

(16)
 
Die Sensitivitätskoeffizienten geben an, wie stark kleine Änderungen im Wert der jeweiligen Eingangsgröße auf den Meßwert durchgreifen. In der Elektrotechik sind sie unter dem Namen Steilheit bekannt. In den meisten Fällen wird es nicht nötig sein, die partiellen Differentiationen in Gleichung (19) wirklich auszuführen. Für zwei einfache, aber häufig auftretende Fälle lassen sich die Sensitivitätskoeffizienten aus der Modellfunktion direkt ablesen:

 

(17)
- Zahlenkonstante, 
   

(18)
 

(19)
- Zahlenkonstante, 
 

 

(20)
 

 

(21)
- relative Standardmeßunsicherheit, die den Eingangswerten beigeordnet ist. 
 
Bachmair hat auf der DGQ-VDI/VDE-Prüfmittelfachtagung in Langen(Hessen) gezeigt [9], wie sich im elektrischen Fall die meisten Modellbildungen meßtechnischer Probleme auf Kombinationen der Formeln (17) bis (21) zurückführen lassen. Seine Überlegungen lassen sich leicht auf andere meßtechnische Gebiete übertragen. Für die verbleibende Bestimmung der Standardmeßunsicherheiten, die den Eingangswerten beigeordnet sind, werden im GUM zwei Verfahren angegeben: die Typ A und die Typ B Ermittlungsmethode.


 
Die Typ B Ermittlungsmethode ist anzuwenden, wenn der vollständige Wert einer Eingangsgröße, d.h. Meßwert und beigeordnete Meßunsicherheit, bekannt sind oder aus der meßtechnischen Erfahrung eine bestimmte Verteilung angenommen werden kann. Im ersten Fall sind der Meßwert und beigeordnete Meßunsicherheit direkt gegeben, man kann sie übernehmen. In Kalibrierscheinen wird die beigeordnete erweiterte Meßunsicherheit angegeben; man erhält die Standardmeßunsicherheit, indem man die erweiterte Meßunsicherheit durch den mitgelieferten Erweiterungsfaktor dividiert. Kann man eine bestimmte Verteilung voraussetzen, wie bei der Auflösung eines digitalen Meßgerätes, verwendet man die entsprechenden Formeln zur Bestimmung der Standardabweichung.


 
Die Typ A Ermittlungsmethode ist anzuwenden, wenn eine Eingangsgröße, etwa die Größe , wiederholt beobachtet wird und dabei unterschiedliche Werte festgestellt werden. Die Auswertung erfolgt dann nach statistischen Methoden. Der Wert ist der arithmetische Mittelwert der Beobachtungen
 

(22)
- beobachtete Werte. 
- Anzahl der gemachten Beobachtungen.
 
Die beizuordnende Standardmeßunsicherheit berechnet sich mit der Formel


 

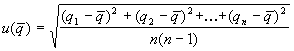(23)
 
Damit die so bestimmte Standardmeßunsicherheit einen statistisch verläßlichen Wert darstellt, sollten mindestens 10 Beobachtungen gemacht werden.


 
Die Gleichungen (13) bis (23) bilden das geschlossene System, das bei der Bestimmung des Meßwertes und der beigeordneten Standardmeßunsicherheit zu benutzen ist. Sie können für Routineauswertungen leicht in Spreadsheet Programme umgesetzt werden. Man kann aber auch komfortablere Auswertprogramme nutzen, die Unsicherheitsanalysen inkl. Protokoll benutzergeführt erstellen. Eine Sammlung von beispielhaften Meßunsicherheitsanalysen findet sich im Supplement S1 zur EAL-R2 [10].


 
Wie das erhaltene vollständige Meßergebnis, aus Meßwert und beigeordneter Standardmeßunsicherheit, anzugeben ist, zeigt folgendes Beispiel für die Kalibrierung eines Gewichtsstückes in drei Formen, jeweils in normaler und relativer Schreibweise:

Bei der numerischen Angabe müssen zwei Tatsachen beachtet werden: Zum einem basiert die Meßunsicherheit auf einer Wahrscheinlichkeitsaussage. Der angegebene Wert sollte daher nicht mehr als zwei signifikante Stellen umfassen. Wahrscheinlichkeiten lassen sich nun mal nur mit einer Genauigkeit von 1-2% angeben (Fussnote 3). Ergeben die Berechnungen mehr als zwei signifikante Stellen, ist mathematisch zu runden. Dabei ist immer aufzurunden, falls sich eine Änderung des Wertes von mehr als 5% ergibt. Zum anderen ist die Präzision des Meßwertes auf die höchstwertigste Stelle der Standardmeßunsicherheit zu begrenzen [2]. Die Schreibweise 3) ist zwar zulässig, sollten bei der Angabe der Standardmeßunsicherheit jedoch nicht benutzt werden, da es leicht zu Verwechslungen mit der erweiterten Meßunsicherheit kommen kann.


 
 
6 Die industriell-ökonomische Sicht : Erweiterte Meßunsicherheit
 
Zum Nachweis der Übereinstimmung eines Meßwertes mit einer Spezifikation ist die Standardmeßunsicherheit nicht geeignet. Sie gibt zwar die Qualität eines Meßergebnisses an, für den Nachweis der Übereinstimmung benötigt man jedoch einen Bereich, der einen hohen Anteil der Werte umfaßt, die mit den Meßbedingungen verträglich sind. In Industrie und Wirtschaft ist deshalb die erweiterte Meßunsicherheit (engl. expanded uncertainty of measurement) gebräuchlich, die aus der Standardmeßunsicherheit abgeleitet wird. Sie ist definiert durch:


 

(24)
 
mit dem Erweiterungsfaktor

(engl. coverage factor) . Der Erweiterungsfaktor wird so gewählt, daß das Unsicherheitsintervall
 

(25)
 
einen hohen Anteil an Werten überdeckt. Der überdeckte Anteil wird Überdeckungswahrscheinlichkeit  (engl. coverage probability) genannt. Damit steht wieder ein Unsicherheitsintervall zur Verfügung, daß für Vergleiche verwendet werden kann. Der Vorteil ist, daß die Berechnung über den Zwischenschritt der Standardmeßunsicherheit ein Verfahren nutzt, das die Häufigkeitsstatistik und Beurteilungswahrscheinlichkeit in sich vereint.


 
Die in der EA zusammengeschlossenen Kalibrierdienste, z.B. DKD, haben sich darauf geeinigt, bei Kalibrierungen für die Berechnung des Erweiterungsfaktors eine einheitliche Überdeckungswahrscheinlichkeit von 95% zu verwenden. Der Erweiterungsfaktor kann aus der Verteilung für jede Überdeckungswahrscheinlichkeit bestimmt werden. Hier kommt der zentrale Grenzwertsatz zur Anwendung. Da in präziseren Messungen i.a. mehrere Einflußgrößen auftreten, ergibt sich für die Werte der Meßgröße meist in guter Näherung eine Normalverteilung. Für sie ergibt sich der bei Kalibrierungen übliche Standardüberdeckungsfaktor .


 
Für die Angabe des vollständigen Meßergebnisses ist nur die Form 3) zulässig, vervollständigt mit der Angabe des verwendeten Erweiterungsfaktors:

Der konventionelle Wägewert des kalibrierten Gewichtsstückes der OIML-Klasse M1 mit dem Nennwert 10 kg beträgt

(10,000 025± 0,000 060) kg
10,000 025 kg± 60,0 mg
oder 10,000 025 kg (1± 6,0* 10-6)
 

 Die angegebene erweiterte Meßunsicherheit ergibt sich aus der Standardmeßunsicherheit durch Multiplikation mit dem Erweiterungsfaktor . Sie entspricht für eine Normalverteilung einer Überdeckungswahrscheinlichkeit von 95%. Die Standardmeßunsicherheit ist in Übereinstimmung mit der Richtlinie EAL-R2 bestimmt worden.
  Bei großen Abweichungen von der Normalverteilung, z.B. wenn ein Unsicherheitsbeitrag im Budget dominiert (@ 90%) oder wenn die einem Eingangswert beigeordnete Standardmeßunsicherheit nach der Typ A Ermittlungsmethode mit nur wenigen Beobachtungen bestimmt wurde, ist eine anderer Erweiterungsfaktor zu wählen. Die Verfahren hierzu finden sich in der EAL-R2 [2] und in den Beispielen des in Arbeit befindlichen Supplements S2.


 
7 Schlußfolgerung
 
Das Verfahren des GUM hat sich schon jetzt als weittragend erwiesen. Die beim Einsatz des gleichen Normals auftretenden Korrelationen zwischen Meßergebnissen bilden den Gegenstand laufender Untersuchungen. Kenntnisse hierüber sind wichtig für die Beurteilung multilateraler Vergleiche. Erste Erfolge in der Behandlung von Hysterese-Effekten bei Kalibrierkurven zeichnen sich ab. Die hier auftretenden Probleme sind von ihrer begrifflichen Behandlung her sehr komplex. Die Ergebnisse werden die Meß- und Prüfmitteltechnik stark beeinflussen.
 
8 Danksagung


 
Ich danke meinen europäischen Kollegen der EA-Task Force für Meßunsicherheit, dem Vorsitzenden Herrn Dr. Wolfgang Wöger und den übrigen Mitgliedern des Meßunsicherheitslenkungsgremiums (MU-L) der PTB für viele anregende und engagierte Diskussionen, die dazu beitrugen, zu verstehen, was das GUM wirklich bedeutet.

9 Fussnoten
 

10 Literatur & Internationale/nationale Empfehlungen

[1] Guide to the Expression of Uncertainty in Measurement,


first edition, 1993, corrected and reprinted 1995, International Organisation for Standardisation (Geneva, Switzerland),
dtsch.: Leitfaden zur Angabe der Unsicherheit beim Messen,
1.Auflage 1995, DIN/Beuth-Verlag
 
[2] EAL-R2 Expression of the Uncertainty of Measurement in Calibration,


requirements document, first edition 1996, European cooperation for Accreditation (of aboratories) (Utrecht, The Netherlands)
dtsch.: DKD-3 Angabe der Meßunsicherheit beim Kalibrieren,
Ausgabe 1998, hrsg. PTB/Wirtschaftsverlag NW
 
[3] International Vocabulary of Basic and General Terms in Metrology,
second edition, 1993,

International Organisation for Standardisation (Geneva, Switzerland),
dtsch.: Internationales Wörterbuch der Metrologie
2.Auflage 1994, DIN/Beuth-Verlag.
 
[4] DIN 1319 Grundlagen der Meßtechnik
Teil 1:

Grundbegriffe
Teil 2: Begriffe für die Anwendung von Meßgeräten
Teil 3: Auswertung von Messungen einer einzelnen Meßgröße, Meßunsicherheit


Teil 4: Auswertung von Messungen, Meßunsicherheit
Deutsches Institut für Normung - Beuth-Verlag
 
[5] Kessel, W: Meßunsicherheit, ein wichtiges Element der Qualitätssicherung,


wird veröffentlicht: PTB-Mitteilungen 108. Jahrgang, Heft 5, Oktober 1998
 
[6] Tischler, K. Entscheidungsregeln zur Festlegung der Übereinstimmung mit
geometrischen Produktspezifikationen (GPS)
MICROTECH 1996, Rahmenprogramm im Auditorium, Frankfurt Oktober 1998
VDI/VDE-Gesellschaft Meß- und Automatisierungstechnik, Düsseldorf 1997.
 


[7] ISO EN DIN 14253, Prüfung von Werkstücken und Meßgeräten durch Messungen,
Teil 1: Entscheidungsregeln für die Feststellung von Übereinstimmung und Nichtübereinstimmung mit Spezifikationen,
Teil 2:

Guide to the estimation of uncertainty of measurement in calibration of
measuring equipment and product specification,
im Entwurf, engl. Draft, herausgegeben vom DIN Deutsches Institut für Normung e.V.
Beuth-Verlag GmbH, Berlin-Wien-Zürich
 
[8] Kessel, W: European and International Standards for Statements of Uncertainty,
Eng.Sci.Educ.J. Vol 7, No 5, October 1998, pp 201-207.


 
[9] Bachmair, H. Meßunsicherheitsbetrachtung für Meß- und Prüfmittel für elektrische Größen.
DGQ & VDI/VDE-GMA Fachtagung "Prüfmittelmanagement und Prüfmittelüberwachung" Langen (Hessen) 28.-29. Oktober 1998


in: VDI Berichte 1445, VDI-Verlag (Düsseldorf, 1998), Seite 167-176.
 
[10] EAL-R2-S1 Supplement 1 to EAL-R2 Expression of the Uncertainty of Measurement in Calibration - Examples,
requirements document, first edition 1996,
European cooperation for Accreditation (of Laboratories)
(Utrecht, The Netherlands)
dtsch.: DKD-3-E1

Angabe der Meßunsicherheit beim Kalibrieren, Beispiele,
Ausgabe 1998, hrsg. PTB/Wirtschaftsverlag NW
 
[11] Kessel, W. Meßunsicherheitsanalyse - fundamentaler Bestandteil der
Prüfmittelüberwachung.
DGQ & VDI/VDE-GMA Fachtagung "Prüfmittelmanagement und Prüfmittelüberwachung" Langen (Hessen) 28.-29. Oktober 1998


in: VDI Berichte 1445, VDI-Verlag (Düsseldorf, 1998), Seite 153-166.

*PDF-Version dieser Seite.

  • Kontakt
  • Links
  • Impressum
  • Suche